SAMSUNG R&D Noida | Onsite OA (2) | April 2025
Summary
This post details a specific coding problem titled 'Car Gathering' encountered during an Onsite Online Assessment at Samsung R&D Noida.
Full Experience
Car Gathering
N cars are randomly placed in the city which needs to be parked at city square P.
All cars need to move together to reach city square. Cars can move up, down, left or right. Cars can move through already visited places, can overlap or cross with routes of other cars.
In 1st drive, all cars will move together 1 step. In 2nd drive, all cars will move together 2 steps. So in t-th drive, all cars move t steps.
It is easier for car to change direction in t-th drive.
For instance on 5-th drive, car can go 2 steps up, 1 step down, again 1 step up and then 1 step right.
(0,0) is the center of the city such that center has length and width of M from boundary.
Find the minimum number of drives required for all the cars to reach city square. If not possible, return -1.
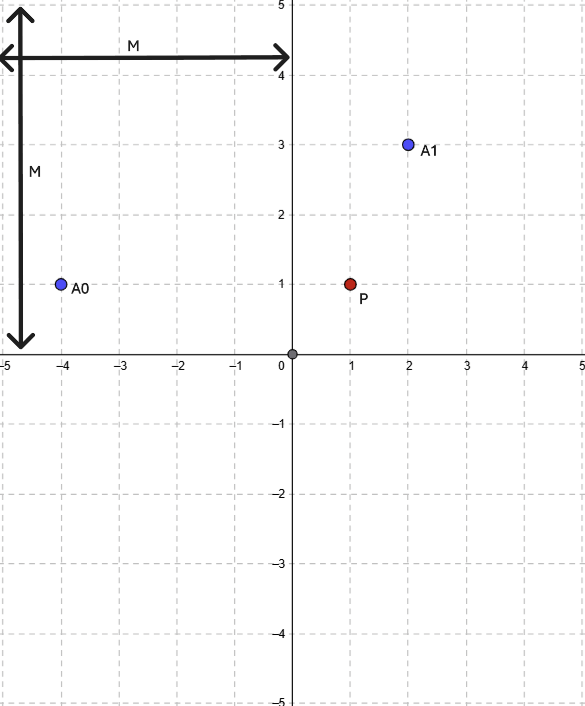
Input
T - no. of test cases(it was mentioned 50) N - no. of cars P - position of city sqaure as (x,y) M - length and width of center of city from boundary A - position of N cars as {(x$$_0$$,y$$_0$$),(x$$_1$$,y$$_1$$),(x$$2$$,y$$2$$)..(x$${n -1}$$,y$${n -1}$$)}
Constraints
1<=N<=100 0<=M<=10$$^{17}$$ -10$$^{17}$$ <= P, x$${i}$$, y$${i}$$ <= 10$$^{17}$$
Output
N = 2 M = 5 P = (1,1) A = {(-4,1),(2,3)} Output = 5 (Total 1+2+...+5=15 steps to reach at P)
N = 5 M = 10 P = (0, 0) A = {(-5,5),(10,8),(1,1),(-9, 9),(8,2)} Output = 7 (Total 1+2+...+7=28 steps to reach at P)
N = 2 M = 3 P = (0, 0) A = {(0, 1),(0,2)} Output = -1 (All cars cannot reach to P at same time. Cars cannot stop mid-way)
Interview Questions (1)
Car Gathering
N cars are randomly placed in the city which needs to be parked at city square P.
All cars need to move together to reach city square. Cars can move up, down, left or right. Cars can move through already visited places, can overlap or cross with routes of other cars.
In 1st drive, all cars will move together 1 step. In 2nd drive, all cars will move together 2 steps. So in t-th drive, all cars move t steps.
It is easier for car to change direction in t-th drive.
For instance on 5-th drive, car can go 2 steps up, 1 step down, again 1 step up and then 1 step right.
(0,0) is the center of the city such that center has length and width of M from boundary.
Find the minimum number of drives required for all the cars to reach city square. If not possible, return -1.

Input
T - no. of test cases(it was mentioned 50) N - no. of cars P - position of city sqaure as (x,y) M - length and width of center of city from boundary A - position of N cars as {(x$$_0$$,y$$_0$$),(x$$_1$$,y$$_1$$),(x$$2$$,y$$2$$)..(x$${n -1}$$,y$${n -1}$$)}
Constraints
1<=N<=100 0<=M<=10$$^{17}$$ -10$$^{17}$$ <= P, x$${i}$$, y$${i}$$ <= 10$$^{17}$$
Output
N = 2 M = 5 P = (1,1) A = {(-4,1),(2,3)} Output = 5 (Total 1+2+...+5=15 steps to reach at P)
N = 5 M = 10 P = (0, 0) A = {(-5,5),(10,8),(1,1),(-9, 9),(8,2)} Output = 7 (Total 1+2+...+7=28 steps to reach at P)
N = 2 M = 3 P = (0, 0) A = {(0, 1),(0,2)} Output = -1 (All cars cannot reach to P at same time. Cars cannot stop mid-way)